Quarantine: Sparsity Can Uncover the Trojan Attack Trigger for Free

Abstract

Trojan attacks threaten deep neural networks (DNNs) by poisoning them to behave normally on most samples, yet to produce manipulated results for inputs attached with a particular trigger. Several works attempt to detect whether a given DNN has been injected with a specific trigger during the training. In a parallel line of research, the lottery ticket hypothesis reveals the existence of sparse subnetworks which are capable of reaching competitive performance as the dense network after independent training. Connecting these two dots, we investigate the problem of Trojan DNN detection from the brand new lens of sparsity, even when no clean training data is available. Our crucial observation is that the Trojan features are significantly more stable to network pruning than benign features. Leveraging that, we propose a novel Trojan network detection regime: first locating a “winning Trojan lottery ticket” which preserves nearly full Trojan information yet only chance-level performance on clean inputs; then recovering the trigger embedded in this already isolated subnetwork. Extensive experiments on various datasets, i.e., CIFAR-10, CIFAR-100, and ImageNet, with different network architectures, i.e., VGG-16, ResNet-18, ResNet-20s, and DenseNet-100 demonstrate the effectiveness of our proposal.

Motivation

How does the model sparsity relate to its train-time robustness against Trojan attacks?

As models usually learn “too well” during training - so much that make various types of attacks possible, backdoor attack (or Trojan Attack) has become a real-life threat to the AI model deployed in the real world. At the same time, extensive research work on model pruning has shown that the weights of an overparameterized model (e.g., DNN) can be pruned without hampering its generalization ability. Combining both lines of research, our story begins with the following question:

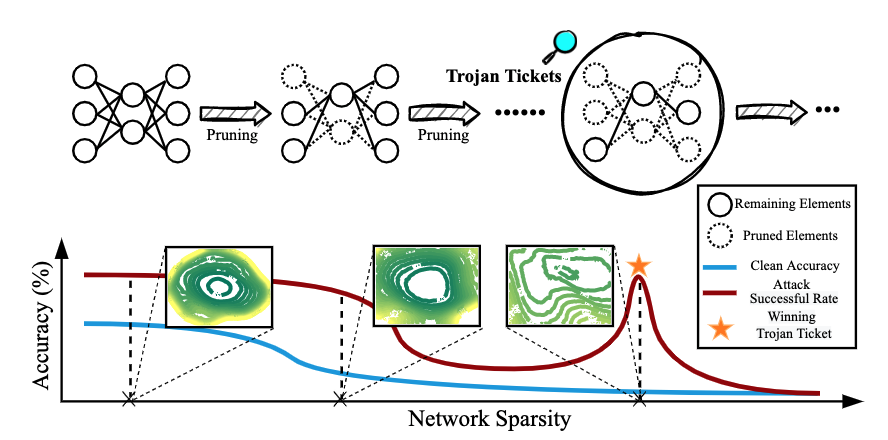
Figure 1. An overview of our proposal: Weight pruning identifies the ‘winning Trojan ticket’, which can be used for Trojan detection and recovery.

Model Pruning v.s. Trojan Attack

We start our research by making an observation on the performance change of a backdoored model as we gradually increase the model sparsity with the model pruning technique. More specifically, we would like to see how the clean accuracy (CA) as well as attack success rate (ASR) will change with respect to the increasing sparsity. We plot the curve of CA and ASR w.r.t. sparsity ratio in Figure 1. Some interesting phenomena we listed below indicate that there is a strong connection between model sparsity and Trojan features.

As ASR is constantly higher than CA, and CA drops much faster than ASR, Trojan features learned by backdoored attacks are significantly more stable against pruning than benign features. Therefore, we assume that “Trojan attacks can be uncovered through the pruning dynamics of the Trojan model”. The question remains: how to leverage the ‘stubbornness’ of the Trojan features to detect the Trojan attack itself?

As we further increase the model sparsity, both ASR and CA reasonably fall to a relatively low level. However, at a certain sparsity level, the ASR surges to a conspicuously high level while the CA remains low, which we term the ‘winning Trojan Ticket’, borrowing the idea from LTH-oriented [1] iterative magnitude pruning. The performance of the winning Trojan Ticket implies that such a model subnetwork preserves the Trojan attack traces while retaining chance-level performance on clean inputs. In other words, it is a ‘purely bad’ subnetwork.

Thus, the existence of the ‘winning Trojan Ticket’ could serve as an indicator of Trojan attacks. However, in real-world applications, it is hard for the users to acquire the ASR (namely the red curve in Figure 1), as the attack information is transparent to the users. Thus, we need to find a substitute indicator for ASR, which does not require any attack information or even clean data.

Trojan Score: Linear Mode Connectivity-based Trojan Indicator

We adopt Linear Mode Connectivity [2] (LMC) to measure the stability of the Trojan ticket

\[\mathcal{S}_{Trojan} = \max_{\alpha \in [0, 1]} \mathcal{E} (\alpha \phi - (1 - \alpha)\phi_{k}) - \frac{\mathcal{\phi} - \mathcal{\phi_k}}{2}\]

Reference

[1] Jonathan Frankle et al. “The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks.” ICLR 2019.

[2] Jonathan Frankle et al. “Linear Mode Connectivity and the Lottery Ticket Hypothesis.” ICML 2020.

[3] Ren Wang et al. “Practical detection of trojan neural networks: Data-limited and data-free cases.” ECCV 2020.